CS61A学习笔记

第一章 Begin

1.1 开始：

1. 本文当中作者简单介绍了python3及一些相关的简单操作：

直接计算，导入包，变量赋值，复合表达式等一些基本的操作

1. 较为关键的部分：

   1. 赋值语句：

      >>> words = set(shakespeare.read().decode().split())
      

      read（读取）、decode（解码）、split（拆分）、set（集合）

   2. 复合表达式：

      >>> {w for w in words if len(w) == 6 and w[::-1] in words}
      {'redder', 'drawer', 'reward', 'diaper', 'repaid'}
      

      3. 调试（debug）：

   3. 增量测试：由可以单独测试的小型模块儿化组件构成，测试编写的所有部分。

   4. 隔离错误：先追踪错误最小的部分（先把错误尽可能的缩小到一定的范围），再尝试着修复问题
   5. 检查假设：明确自己的假设，然后集中debug验证自己的假设（程序实际的执行目标）
   6. 咨询他人：让别人查看你的代码的问题

1.2 编程要素：

1. 注意编程语言的三种机制：
2. 基本表达式和语句：最简单的个体
3. 组合方法：由简单的元素组合构建复合元素
4. 抽象方法： 命名重复的元素，并且将其作为单元进行操作

在编程当中关注函数和数据，编程语言都是对于函数和数据进行组合和抽象

1.2.1 表达式

1. 数值表达式：(输出即为键入值)

>>> 42
42

1. 复合表达式（数值和运算符的组合形式（中缀表达式））：(输出为运算结果)

   >>> -1 - -1
   0
   >>> 0+1-1+1-1
   >>>0
   

1.2.2 调用表达式

将参数传入一些函数

>>>max(8,2.2)
8

>>>pow(100,2)
10000

函数符号的优点：

1. 函数名在参数前，所以函数可以接收任意数量参数，不会产生歧义

>>>max(1,-2,3,-4)
3

1. 其次，函数可以直接扩展为嵌套（nested）表达式，其元素本身就是复合表达式。不同于中缀复合表达式，调用表达式的嵌套结构在括号中是完全明确的。

   >>> max(min(1,-2),min(pow(3,5),-4))
   -2
   

   Ps：这种嵌套的深度（理论上）没有任何限制，Python 解释器可以解释任何复杂的表达式。但人类很快就会被多层嵌套搞晕，所以作为一个程序员，你的一个重要目标就是：构造你自己、你的编程伙伴和其他任何可能阅读你代码的人都可以解释的表达式。

2. 数学符号在形式上多种多样：星号表示乘法，上标表示幂指数，水平横杠表示除法，带有倾斜壁板的屋顶表示平方根，而其中一些符号很难被输入！但是，所有这些复杂事物都可以通过调用表达式的符号来进行统一。Python 除了支持常见的中缀数学符号（如 + 和 -）之外，其他任何运算符都可以表示为一个带有名称的函数。

1.2.3 导入库函数

例如：math模块：

>>>from math import sqrt
>>> sqrt(256)
16.0

operator模块中的中缀运算函数：

>>>from operator import add,sub,mul#加法，减法，乘法
>>>add(14,28)
42
>>>sub(100,mul(7,(add(8,4)))

import 语句需要指定模块名称（例如 operator 或 math），然后列出要导入该模块里的具名函数（例如 sqrt）。 一个函数被导入后就可以被多次调用。

特殊的变量名：例如max可以重新绑定成为一个变量：

>>>max =5
>>>max
5

Ps: 绑定完之后max只能作为变量使用调用max(2,3,4)将报错

执行赋值语句时，Python 会先求解 = 右侧的表达式，再将结果与左侧的名称绑定，所以可以在右侧表达式中引用一个已绑定的变量。

>>> x = 2
>>> x = x + 1
>>> x
3

还可以在单个语句中为多个变量分配值，左右都用逗号隔开。

>>> area, circumference = pi * radius * radius, 2 * pi * radius
>>> area
314.1592653589793
>>> circumference
62.83185307179586

更改一个变量的值不会影响其他变量。即使下列代码中 area 的值由最初定义的 radius 绑定，但改变 radius 的值并不能更新 area 的值，我们需要另一个赋值语句来更新它。

>>> radius = 11
>>> area
314.1592653589793
>>> area = pi * radius * radius
380.132711084365

对于多重赋值，所有 = 右边的表达式都会先求值，然后再与左边的名称绑定。在这个规则下，我们可以在单个语句内交换两个变量的值。

>>> x, y = 3, 4.5
>>> y, x = x, y
>>> x
4.5
>>> y
3

本章的目标之一是在“以程序的角度思考”中隔离其他的问题，举一个恰当的例子，就是思考一下在求解嵌套表达式时，解释器自身的操作过程。

为了求值一个表达式，Python 将执行以下操作：

• 求解运算符子表达式和操作数子表达式
• 然后将操作数子表达式的值作为运算符子表达式的函数的参数

这个简单的过程也说明了有关流程的一些要点。第一步规定：为了求出调用表达式，必须首先求出其他表达式。因此，求值程序本质上是递归（recursive）的，也就是说它会自己调用自己作为步骤之一。

例如，此式需要应用四次求值过程。

>>> sub(pow(2, add(1, 10)), pow(2, 5))
2016

如果把每个需要求解的表达式都抽出来，我们可以看到这个求值过程的层次结构。

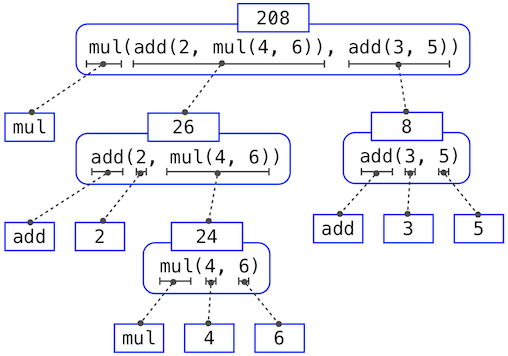
这个图叫做表达式树，在计算机科学中，树通常从上到下增长。树中每个点的对象都叫做节点。这里节点分别是表达式和表达式的值。

求解根节点（即顶部的完整表达式），需要首先求解子表达式，也就是分支节点。叶子节点（也就是没有分支的节点）表示函数或数值。内部节点有两部分：我们想要应用的求值规则的调用表达式，以及该表达式的结果。观察这棵树的求解过程，我们可以想象操作数的值会向上流动，从叶子节点开始一步步向上组合。

接下来，观察第一步的重复应用，将我们带到我们需要求解的原始表达式，而不是调用表达式，例如数字（例如 2）和名称（例如 add）。 我们规定基本逻辑为：

• 数字的值就是它们所表示的数值
• 名称的值是环境中关联此名称的对象

注意环境在决定表达式中的符号意义上有重要作用。在 Python 中，不指定任何环境信息去谈论一个值是没有意义的，例如名称 x 和 add。环境为求解提供了上下文信息，对理解程序执行过程有着重要作用。

>>> add(x, 1)

这个求解步骤并不能对所有 Python 代码求值，它仅能求解调用表达式、数字和名称。例如，它并不能处理赋值语句。

>>> x = 3

因为赋值语句的目的是将名称与值绑定，它并不返回值，也不应用参数去求解函数。也就是说，赋值语句不被求解但“被执行”，它们只是做出一些改变但不产生值。每种类型的表达式或语句都有自己的求解或执行过程。

注意：当我们说“一个数字求解为一个数值”时，实际上是 Python 解释器将数字求解为数值，是解释器赋予了编程语言这个意义。鉴于解释器是一个始终表现一致的固定程序，我们就可以说数字（以及表达式）会在 Python 程序的上下文中被求解为值。